Como construir um triângulo regular a partir da medida do lado.

by Roberto M.

Já vimos o que é polígono e sabemos que triângulo é um polígono de três lados.

Aprendemos também, que para o polígono ser chamado “regular”, todos os seus lados e todos os seus ângulos têm que ser congruentes, ou seja, suas medidas têm que ser iguais.

Em outro artigo, mostramos como dividir uma circunferência dada em três partes iguais e com isso, inscrever um triângulo regular nela.

Hoje, vamos fazer um pouco diferente. Iremos mostrar como é a construção de um triângulo regular a partir da medida de seu lado.

Então, mãos à obra com lápis, papel, régua e compasso.

CONSTRUÇÃO DE UM TRIÂNGULO REGULAR SABENDO A MEDIDA DO LADO

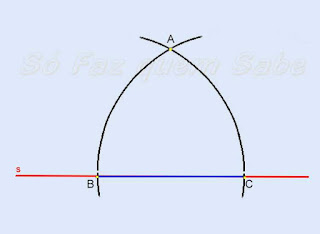
1) Primeiramente, com a régua e o lápis, desenhemos uma reta “s” no papel.

2) Agora marquemos nessa reta a medida desejada do lado do triângulo, através do segmento de reta BC. Desse modo, já temos determinados dois vértices do triângulo, o B e o C.

3) Pegamos o compasso, e com uma abertura de raio igual à medida do segmento BC, colocamos a ponta seca no ponto C e traçamos um arco de circunferência.

4) Procedendo da mesma maneira, agora com a ponta seca em B e com o mesmo raio BC, traçamos outro arco de circunferência de modo que intersecte o arco anterior. Nessa intersecção será determinado o ponto A.

5) O ponto A é o terceiro vértice do triângulo. Ao unir os pontos A, B e C obteremos o triângulo regular que pretendíamos.

Artigos Recomendados:

• Noções Fundamentais da Geometria. Ideias de ponto, reta e plano.
• Circunferência. Definição e Construção.
• Poligonal. Uma linha não linear.
• Conceito de ângulo e de sua medida.
• Diferenças entre linha, curva e poligonal. Regiões geométricas.