Classificação de um triângulo quanto aos lados: equilátero, isósceles e escaleno.

by Roberto M.

O que é triângulo equilátero? O que é triângulo isósceles? O que é triângulo escaleno?

Já vimos o que é um polígono e sabemos que triângulo é um polígono de três lados.

Vimos, também, que um triângulo tem vários elementos, tais como: os vértices, os ângulos internos, os ângulos externos e os lados.

Mas o que acontece quando comparamos, entre si, os lados de um triângulo qualquer?

É exatamente nessa comparação que vamos obter a classificação do triângulo quanto aos lados.

Ao fazer essa comparação, podem ocorrer três situações:

1) Os três lados do triângulo são congruentes, ou seja, têm medidas iguais;

2) Dois lados são congruentes (com medidas iguais) e o terceiro lado tem medida diferente desses dois;

3) Os três lados têm medidas diferentes entre si, ou seja, dois lados quaisquer não são congruentes.

A partir de cada uma dessas três situações, definimos os nomes de cada um dos tipos de triângulo quando usamos os lados para classificá-los.

EQUILÁTERO

No primeiro caso, quando os três lados de um triângulo qualquer são congruentes, dizemos que esse triângulo é Equilátero.

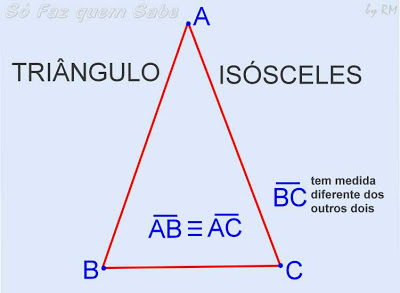
ISÓSCELES

No segundo caso, quando dois lados quaisquer são congruentes e o terceiro tem medida diferente, dizemos que esse triângulo é Isósceles.

ESCALENO

No terceiro caso, quando os três lados têm medidas diferentes entre si, dizemos que o triângulo é Escaleno.

Artigos Recomendados:

• Noções Fundamentais da Geometria. Idéias de ponto, reta e plano.
• Semi-Reta e Segmento de reta. Avançando nos conceitos.
• Mediatriz de um segmento de reta. Aprendendo a traçar e a obter o ponto médio.
• Como construir um triângulo regular a partir da medida do lado.
• Dividindo a circunferência em três partes iguais.