Construção de um triângulo qualquer. Condição de existência de um triângulo.

by Roberto M.

Vimos outro dia, como construir um triângulo regular a partir da medida de seu lado e, como o triângulo regular é aquele que tem todos os lados iguais, sabendo-se a medida de um lado, é lógico, se sabe a medida dos três lados.

No caso dos três lados terem medidas diferentes, o processo de construção é semelhante, mudando apenas as aberturas do compasso de acordo com as medidas dos lados.
 

Pode-se considerar a construção do triângulo regular como um caso particular do caso geral que é a construção de um triângulo qualquer.

Vamos, praticamente, mostrar outra vez a construção de um triângulo, só que de uma maneira mais geral. Entretanto, o mais importante nesse artigo não é a construção propriamente dita, mas sim a condição de existência de um triângulo (a desigualdade triangular) que comentarei logo a seguir.

CONSTRUÇÃO DE UM TRIÂNGULO A PARTIR DA MEDIDA DOS LADOS

Como exemplo, vamos construir um triângulo ABC, cujos lados medem:

a = 7 unidades (BC)   ;   b = 5 unidades (AC)   ;   c = 6 unidades (AB)

1) Podemos começar pelo lado que desejarmos. Vamos começar pelo lado BC. Então, tracemos um segmento BC de medida a = 7 unidades.

2) Colocamos a ponta seca do compasso no ponto C e traçamos um arco de medida b = 5 unidades.

3) Colocamos a ponta seca do compasso no ponto B e traçamos um arco de medida c = 6 unidades de modo que esse arco intersecte o anterior.

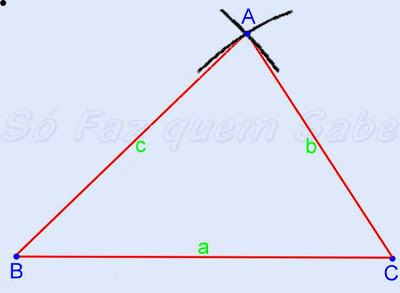
4) A intersecção desses dois arcos determina o ponto A, terceiro vértice do triângulo.

5) Ligando-se os três vértices construímos o triângulo desejado.

CONDIÇÃO DE EXISTÊNCIA DE UM TRIÂNGULO

Da maneira descrita acima, teoricamente, podemos construir triângulos com quaisquer medidas de lados. Entretanto, existem certas composições de medidas com as quais não dá para construir um triângulo.

Tente, por exemplo, construir um triângulo com os lados medindo:

a = 7 unidades  ;  b = 4 unidades   e   c= 2 unidades.

Seguindo os passos de construção acima, obtemos:

Como podemos observar, não existe triângulo com os lados medindo 7 unidades, 4 unidades e 2 unidades.

Para justificar esse acontecimento, vamos enunciar uma propriedade que é justamente a condição de existência de um triângulo:

Um triângulo qualquer, para existir, tem de ter cada um de seus lados com uma medida menor que a soma das medidas dos outros dois lados.

Em outras palavras:

Em qualquer triângulo, cada lado é menor que a soma dos outros dois.

Portanto, dado um DABC  com medidas a(BC), b(AC) e c(AB), o triângulo só existirá se obedecer às seguintes relações simultaneamente:

a < b + c

b < a + c

c < a + b

Essas são as chamadas desigualdades triangulares.

Assim, para sabermos se um triângulo existe, conhecendo-se as medidas dos lados, basta comparar a medida do maior lado com a soma das medidas dos outros dois.

Artigos Recomendados:

• Os elementos de um triângulo. Vértices, lados e ângulos.
• Classificação de um triângulo quanto aos lados: equilátero, isósceles e escaleno.
• Dividindo a circunferência em três partes iguais.
• Noções Fundamentais da Geometria. Idéias de ponto, reta e plano.
• Semi-Reta e Segmento de reta. Avançando nos conceitos.