by Roberto M.
Em
um artigo anterior, tivemos a oportunidade de conhecer o conjunto dos números naturais (N),
surgido da necessidade que o homem tinha de contar objetos. Depois, em outro
artigo, conhecemos o conjunto dos números inteiros (Z),
onde apareceram os números negativos, ou seja, os números menores que zero, que
podem representar, por exemplo, as temperaturas mais frias que zero
grau.
Neste
artigo, iremos evoluir um pouco mais e começar a estudar um novo tipo de
números, os chamados números
fracionários, que representam as partes de um inteiro.
INTRODUÇÃO
Como
definição, podemos dizer que:
“Números fracionários são números que
representam uma ou mais partes de uma unidade que foi dividida em partes
iguais.”
Para
tornar mais clara essa definição, vamos explicá-la com um exemplo
prático:
Vamos
supor que eu, minha esposa e meus dois filhos (4 pessoas) compramos uma pizza
para o jantar. A pizzaria entregou a pizza já cortada em 8 partes
iguais.
Cada
um de nós comeu um pedaço. Em seguida eu e meu filho repetimos e comemos mais um
pedaço cada um.
Podemos
observar, nesse exemplo, que a pizza inteira representa a unidade e que as
pessoas receberam frações dessa
unidade. Eu e meu filho, por exemplo, comemos, cada um, duas das oito partes. Já
minha esposa e minha filha comeram, cada qual, uma das oito
partes.
Para
representar essas frações foram “inventados” os números
fracionários.
REPRESENTAÇÃO DOS NÚMEROS FRACIONÁRIOS
Os
números fracionários são representados por dois números inteiros separados por
um traço horizontal (que também é chamado de traço de fração), sendo que o
número de baixo deverá sempre ser diferente de zero.
Exemplos:
Generalizando:
Chama-se
fração todo par de números inteiros
Leia-se
a
sobre b, com b
diferente de zero.
Os
dois números inteiros, a e b, são os termos que compõem uma fração e são
chamados numerador e denominador.
-
O segundo número (b) é o denominador e indica em quantas partes
iguais a unidade foi dividida.
-
O primeiro número (a) é o numerador e indica quantas das partes
iguais tomamos da unidade dividida.
No
nosso exemplo da pizza, eu comi duas partes de uma pizza que havia sido dividida
em oito partes iguais, ou seja, o inteiro foi dividido em oito partes e eu
peguei duas dessas partes.
Logo
eu peguei
da
pizza.
LEITURA DOS NÚMEROS FRACIONÁRIOS
Para
fazer a leitura de uma fração, devemos começar a ler pelo número que está no
numerador (em cima), para em seguida, ler o denominador (em
baixo).
A
leitura do denominador depende do número de partes em que foi dividida a
unidade, sendo que para cada caso, cada parte recebe um
nome.
Veja
na tabela abaixo, o nome de cada parte relativa às várias
divisões:
NÚMERO DE PARTES
EM QUE FOI DIVIDIDA
A UNIDADE
|
NOME DE CADA
PARTE
|
2
|
MEIO
|
3
|
TERÇO
|
4
|
QUARTO
|
5
|
QUINTO
|
6
|
SEXTO
|
7
|
SÉTIMO
|
8
|
OITAVO
|
9
|
NONO
|
10
|
DÉCIMO
|
11
|
ONZE AVOS
|
12
|
DOZE AVOS
|
13
|
TREZE AVOS
|
100
|
CENTÉSIMO
|
1000
|
MILÉSIMO
|
Como
regra geral, podemos dizer o seguinte:
Para
fazer a leitura dos números
fracionários, devemos começar a ler pelo número que está no numerador, para, em seguida, ler o
número que está no denominador
acrescido da palavra avos,
exceto quando o denominador se apresentar com os números 2; 3; 4; 5; 6; 7; 8; 9;
10 ou potencias de 10.
Nesses casos, ele tem os nomes especiais citados na tabela acima.
Exemplos de leitura:
Até aqui, descobrimos o que é uma fração, como representar os números fracionários, quais os nomes dos termos de uma fração e como se faz a leitura de um número fracionário. No próximo artigo, falaremos sobre os vários tipos de frações. Acompanhem.


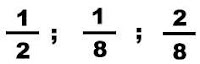


muito bom
ResponderExcluirMuito bom
ResponderExcluirMuito bom1
ResponderExcluirrecomendo.
Parabéns!
Muito bom !
ResponderExcluirOtimo
ResponderExcluirAdorei
ResponderExcluirBom
ResponderExcluirMuito bom o conteúdo !
ResponderExcluirBom
ResponderExcluirgostei muito das informações.
ResponderExcluirentende mas um pouco de matematica bom.
ResponderExcluirMuito BOM!
ResponderExcluirÓtima explicação. Muito obrigado!
ResponderExcluirMuito bem instruído. Mais facilidade de aprendizagem. Estou me acostumando com a matéria que sempre precisei enfrentar para aprender. Muito obrigado pela instrução.
ResponderExcluirMuito bom participar. Adquiro mais conhecimento. Muito obrigado!
ResponderExcluirSer aluno da Faculdade Serra Dourada se aprende muito. Parabéns!
ResponderExcluirCompensa estudar para aprender mais. Muito obrigado!
ResponderExcluirBOM
ResponderExcluirRECOMENDO, PORQUE É MUITO IMPORTANTE!
ResponderExcluirMuito importante
ResponderExcluirexplicação maravilhosa
ResponderExcluirPerfeito
ResponderExcluirBoooom
ResponderExcluirÓtimo
ResponderExcluirMuito bom
ResponderExcluirMuito bom a explicação perfeito adorei parabéns
ResponderExcluir