Octógono Regular e a circunferência dividida em oito partes iguais.

by Roberto M.

Como é que se constrói um octógono regular? Qual é o método utilizado para se dividir uma circunferência em oito partes iguais? Como se faz para inscrever um octógono regular numa circunferência?

Quando dividimos uma circunferência em oito partes iguais, os oito pontos que achamos são também os vértices do octógono inscrito na circunferência.

Já aprendemos em outros artigos, como traçar retas perpendiculares e, também, como traçar a bissetriz de um ângulo.

É bom relembrar esses conceitos, pois iremos utilizá-los na construção do octógono.

Mas vamos, então, ao passo a passo dessa construção geométrica. Peguemos lápis, papel, régua e compasso para começar a traçar.

PASSO 1

Primeiro traçamos a circunferência. Marcamos um ponto C no papel e, com um compasso, traçamos uma circunferência com centro nesse ponto C e com um raio qualquer.

PASSO 2

Agora vamos começar a dividi-la. Com a régua traçamos um diâmetro da circunferência e marcamos os pontos A e B.

PASSO 3

Em seguida, vamos traçar outro diâmetro, perpendicular ao diâmetro AB. Utilizando-nos da técnica aprendida no artigo “Retas perpendiculares que se cruzam num ponto dado” tracemos uma perpendicular à reta AB que passe pelo ponto C.

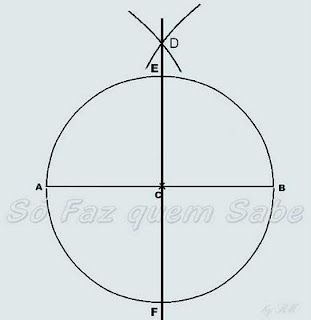
Pegamos o compasso e, com um raio maior que BC, com centro em A e B, fazemos dois arcos acima da circunferência que ao se interceptarem definirão o ponto D.

Com a régua, traçamos a reta que passa pelos pontos D e C que é a perpendicular que queríamos. Com isto, estão definidos os pontos E e F (intersecção da reta DC com a circunferência).

PASSO 4

Nesse estágio, já dividimos a circunferência em quatro partes iguais. Agora, basta dividir cada uma dessas partes ao meio que teremos as oito partes iguais desejadas.

Para isso, usaremos a técnica aprendida no artigo “Bissetriz de um ângulo. Aprenda a traçar”.

Pegamos o compasso. Com a ponta seca no ponto C, e com uma abertura qualquer, traçamos uma semi-circunferência que intersecte os lados dos ângulos formados pelos diâmetros, definindo os pontos 1, 2 e 3.

PASSO 5

Pegamos o compasso e, com um raio maior que a distância de 1 a 2, com centro em A, E e B, fazemos quatro arcos acima da circunferência que ao se interceptarem definirão os pontos X e Y.

PASSO 6

Com a régua, traçamos a reta que passa pelos pontos X e C e, também, a reta que passa pelos pontos Y e C. Essas duas retas são as bissetrizes dos ângulos que dividiam a circunferência em quatro partes, que agora foram divididos ao meio. Essas duas bissetrizes definiram os pontos G, H, I e J (intersecção das retas com a circunferência).

PASSO 7

Os pontos A, J, E, G, B, H, F e I dividem a circunferência em oito arcos congruentes. São também os vértices do octógono inscrito. É só uni-los para obtermos o octógono desejado.

Artigos Recomendados:

• Noções Fundamentais da Geometria. Ideias de ponto, reta e plano.
• Semi-Reta e Segmento de reta. Avançando nos conceitos.
• Circunferência. Definição e Construção.
• Construção do Heptágono regular. Dividindo a circunferência em sete partes iguais.
• Os elementos de um triângulo. Vértices, lados e ângulos.