by Roberto M.
No estudo da geometria, depois que aprendemos os conceitos iniciais de ponto, reta e plano, não demora muito para
que alguém comente sobre os tais pontos notáveis de um triângulo. Hoje
vou falar de um deles, o Incentro do triângulo.
De início, quero dizer que o incentro está relacionado com as bissetrizes de
um triângulo, ou seja, para se obter o incentro, é necessário que se determine,
antes, as bissetrizes do triângulo.
Sabemos que bissetriz interna de um ângulo é a semi-reta que tem origem no
vértice, é interna ao ângulo e o divide ao meio, ou seja, em dois ângulos
congruentes.
No artigo “Bissetriz de um ângulo. Aprenda a
traçar.” aprendemos como traçá-la. Vá lá, leia e
relembre como se traça a bissetriz de um ângulo.
BISSETRIZES E INCENTRO
Como o triângulo tem 3 ângulos, consequentemente, cada triângulo tem 3
bissetrizes internas.
Acontece que, ao traçarmos as três bissetrizes do triângulo, constataremos
que elas se cruzam em um único ponto, ou seja, as três bissetrizes têm um ponto
em comum.
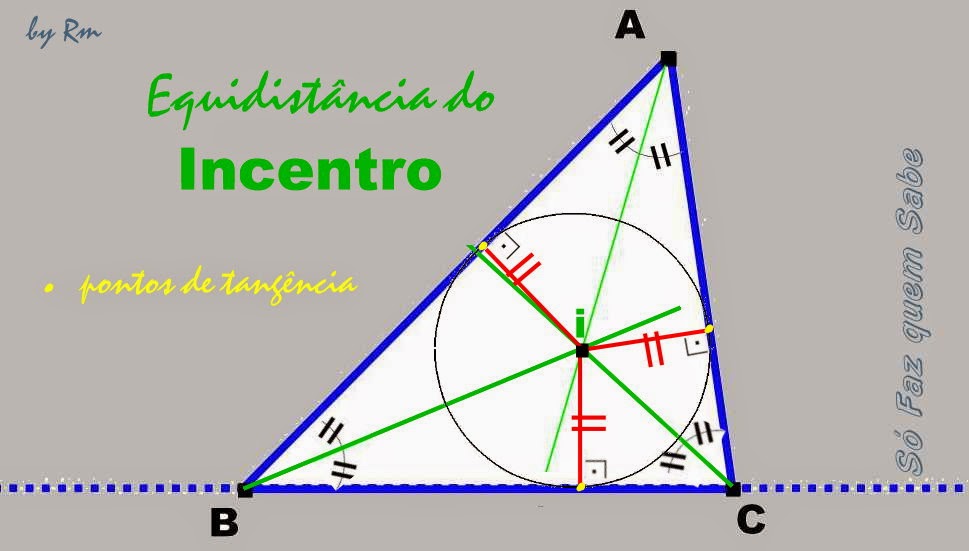
É a esse ponto de encontro das três bissetrizes (i) que damos o
nome de Incentro.
Portanto, dizemos que:
Incentro de um triângulo é o ponto de encontro (cruzamento ou intersecção)
das três bissetrizes do triângulo.
CIRCUNFERÊNCIA INSCRITA NUM TRIÂNGULO
Mas, esse tal de incentro tem uma propriedade interessante.
Como cada bissetriz divide o ângulo ao meio, qualquer ponto localizado nessa
bissetriz terá a mesma distância a qualquer um dos lados do ângulo.
Como o incentro é a intersecção das três bissetrizes do triângulo, ele será
equidistante (mesma distância) aos três lados do triângulo.
Sendo assim, podemos concluir que o Incentro será o centro da circunferência
inscrita nesse triângulo, ou seja, da circunferência que tangenciará,
internamente, os três lados do triângulo ao mesmo tempo.
No próximo artigo falarei do circuncentro, um outro ponto
notável do triângulo. Acompanhem.
Artigos Recomendados:
- As Cevianas notáveis e especiais de um triângulo: Altura, Mediana e Bissetriz.
- Os elementos de um triângulo. Vértices, lados e ângulos.
- Mediatriz de um segmento de reta. Aprendendo a traçar e a obter o ponto médio.
- MEDIANAS quando cruzam, formam o BARICENTRO do triângulo, um ponto notável.
- Das ALTURAS do triângulo obtemos o ORTOCENTRO, um ponto notável.





Nenhum comentário:
Postar um comentário