No artigo “Introdução à Teoria dos Conjuntos” tivemos uma noção geral sobre os principais
conceitos da teoria dos conjuntos.
Lá vimos o que é conjunto, o que é subconjunto e o que é elemento de um
conjunto. Vimos, também, como se nomeia e como se representa um conjunto, além
de mostrar alguns símbolos e falar sobre as relações de pertinência e de
inclusão existentes entre conjuntos e seus elementos.
Hoje, vamos complementar aquele artigo. Daremos mais alguns conceitos e falaremos sobre as principais operações que podemos executar com conjuntos.
FORMAS DE REPRESENTAÇÃO DE UM CONJUNTO
As principais formas de representação de um conjunto são:
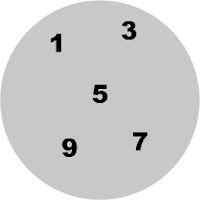
1 - por extenso:
A = {1, 3, 5, 7, 9};
2 - por descrição:
A = {x | x é um número ímpar de um só algarismo};
3 - por diagrama de Venn-Euler:
NÚMERO DE ELEMENTOS DE UM CONJUNTO
Como já vimos, conjunto é uma coleção de objetos de qualquer natureza, ou
seja, é um agrupamento de elementos com características pré-definidas.
Desse modo, poderemos ter conjuntos:
1- Com um número finito de elementos (conjunto finito), como o conjunto A
mostrado no exemplo acima,
2- Ou formados por infinitos elementos (conjunto infinito), como qualquer
conjunto numérico (conjunto dos números inteiros, conjunto dos números reais,
etc.).
3- Além disso, poderemos ter um conjunto unitário, quando possuir
apenas um elemento:
B = {fevereiro}
B = {x | x é mês com menos de 30 dias}
4- Ou um conjunto vazio,
caso não exista nenhum elemento que preencha a característica procurada:
C =
{x | x é par e ímpar}
C = {} ou Ǿ
5- Como nomenclatura, devemos lembrar, ainda, do conjunto
universo; aquele que deve conter todas as soluções possíveis nas resoluções de
problemas e equações.
IGUALDADE ENTRE DOIS CONJUNTOS
-Dois conjuntos A e B são iguais se possuírem os mesmos elementos.
-Dizemos que dois conjuntos A e B são iguais quando A está contido em B e
também B está contido em A; ou seja:
A=B é o mesmo que A⊂B e B⊂A.
-Dizemos que dois conjuntos A e B são diferentes quando existir algum
elemento que é de um e não é do outro e indicamos
A≠B.
Exemplo:
1 - Sejam os conjuntos: A= {1, 2, 3}; B= {4, 5, 6}; C= {3, 1, 2}
Podemos dizer que:
A=C
A≠B; B≠C
REUNIÃO OU UNIÃO DE CONJUNTOS
-Reunião ou União de dois conjuntos A e B é o conjunto formado por todos os
elementos de A e por todos os elementos de B e somente por eles.
- Usamos o símbolo ⋃ para indicar reunião entre dois conjuntos
Exemplo:
1 - Sejam os conjuntos A= {1, 2, 3}; B= {4, 5, 6}; C= {3, 1, 2}; D= {1, 2}
Então teremos:
A⋃B= {1, 2, 3, 4, 5, 6};
B⋃C= {1, 2, 3, 4, 5, 6};
A⋃C= {1, 2, 3};
A⋃D= {1, 2, 3}
INTERSEÇÃO DE CONJUNTOS
- Intersecção ou Interseção de dois conjuntos A e B é o conjunto formado com os elementos
que estão simultaneamente nos dois conjuntos A e B.
- Usamos o símbolo ⋂ para indicar intersecção entre dois conjuntos.
Exemplo:
1 - Sejam os conjuntos A= {1, 2, 3}; B= {4, 5, 6}; C= {3, 1, 2}; D= {1, 2}
Então teremos:
A⋂C= {1, 2, 3};
A⋂D= {1, 2}
CONJUNTOS DISJUNTOS
-Conjuntos disjuntos são aqueles que não têm nenhum elemento em comum, ou
seja, sua interseção é o conjunto vazio.
Exemplo:
1 - Sejam os conjuntos A= {1, 2, 3}; B= {4, 5, 6}
Então teremos:
A⋂B= {} ou Ǿ;
DIFERENÇA ENTRE CONJUNTOS
- Diferença entre dois conjuntos A e B (A – B) é o conjunto formado pelos
elementos exclusivos do conjunto A, ou seja, retira-se de A os elementos que são
comuns com B.
- A representação da diferença entre A e B é: A – B
- Note que A - B é diferente de B – A
- A diferença entre B e A (B – A) é o conjunto formado pelos elementos
exclusivos de B, ou seja, retiram-se de B os elementos comuns com A
Exemplo:
1 – Sejam os conjuntos: A = {0, 1, 2, 3, 4} e B = {2, 3, 4, 5, 6};
A diferença entre A e B é o conjunto formado pelos elementos exclusivos de A,
isto é, retira-se de A o que for comum com B.
A – B = {0, 1}
A diferença
entre B e A é o conjunto formado pelos elementos exclusivos de B, isto é,
retira-se de B o que for comum com A.
B – A = {5, 6}
CONJUNTOS COMPLEMENTARES
- Conjunto complementar é uma modalidade de diferença de conjuntos, que
ocorre quando um conjunto está contido em outro.
- Complementar de um conjunto B em relação a um conjunto A (se B⊂A) é o
conjunto formado pelos elementos de A que não pertencem a B.
- Usamos um traço sobre o nome do conjunto para indicar complementar. Assim,
dados os conjuntos A e B, com B⊂A teremos que B é
o complementar de B em A.
Exemplo:
1 - Sejam os conjuntos: A= {1, 2, 3, 4, 5, 6, 7, 8, 9, 0}; B= {1, 2, 3, 4, 5}
Então teremos:
B = {6, 7, 8, 9, 0}
No próximo artigo falarei sobre “O Produto Cartesiano de Conjuntos”, uma
outra operação que se faz com conjuntos, não sem antes falar sobre "O Plano Cartesiano e os Pares ordenados.". Acompanhem.
Artigos Recomendados:
- Múltiplos de um número natural.
- Operações com números não exatos e envolvendo algarismos significativos.
- Conjunto dos Números Inteiros. O conjunto Z.
- Frações e Números fracionários. Introduzindo o conceito.
- Tipos de Frações: próprias, impróprias e aparentes. Forma mista de um número.
- Como transformar uma fração imprópria em número misto e vice-versa.





Nenhum comentário:
Postar um comentário