by Roberto M.
É muito comum no nosso dia a dia, ao lermos jornais ou vermos televisão, nos
depararmos com gráficos.
Para interpretá-los, temos a necessidade de saber os conceitos de plano
cartesiano.
Embora já tivesse sido usado por matemáticos anteriores, quem formalizou o
conceito do sistema cartesiano foi o filósofo e matemático francês René
Descartes (1596 – 1650), em sua obra Géométrie escrita em 1637.
Como
ele associava a geometria à álgebra, esta foi a forma que encontrou para
representar graficamente expressões algébricas.
Inclusive, o nome “cartesiano” é uma homenagem ao mentor do sistema, pois se
origina da palavra “Cartesius”, que é o nome Descartes, em latim.
Vamos, então, começar a entender os conceitos do plano cartesiano:
a) Pares Ordenados
Ao lermos ou ouvirmos que algumas coisas são, ou estão, “ordenadas” iremos,
sem dúvida, relacionar com coisas que guardam certa ordem, ou seja, a posição em
que se encontram tem importância no contexto geral em que estão inseridas.
Sendo assim, podemos dizer que um par (duas coisas) é ordenado quando a
posição de cada um dos componentes tem influência na definição do par.
A ordem é relevante em um par ordenado.
Um PAR ORDENADO, denotado por (a, b), é um par de elementos onde
a é o primeiro elemento e b é o segundo elemento do par. Note que,
por ser ordenado, o par (a, b) é diferente do par (b, a).
É importante dizer que um conjunto de coisas individuais é diferente de um
conjunto de pares.
Assim um conjunto {a, b} (de dois elementos) é diferente de um
conjunto {(a, b)} (conjunto unitário).
Logo, os conjuntos {a, b} e {b, a} são iguais, mas os pares ordenados (a, b)
e (b, a) são diferentes.
Exemplos:
Se considerarmos os algarismos 2 e 3, teremos que o conjunto desses dois
algarismos seria {2, 3} = {3, 2}.
Agora, se considerarmos os números de dois algarismos formados por 2 e 3
teremos um conjunto de pares ordenados.
(2, 3) é um par ordenado em que o primeiro elemento é 2 e o segundo é 3;
(3, 2) é um par ordenado em que o primeiro elemento é 3 e o segundo é 2;
Note que os pares (2, 3) e (3, 2) diferem entre si pela ordem de seus
elementos, ou seja, eles formam os números 23 ou 32, dependendo da ordem.
b) Plano Cartesiano Ortogonal
Vamos ver como Descartes idealizou o plano cartesiano para conseguir
representar graficamente as suas expressões algébricas.
1 - Primeiramente, ele forma um plano através de duas retas perpendiculares que se cruzam em um determinado
ponto, de tal modo que uma seja horizontal e outra seja vertical.
Como essas retas são perpendiculares, ou ortogonais, o plano formado por elas
ficou conhecido como plano cartesiano ortogonal.
2 – Em seguida, ele orienta essas retas e as chama de eixos. Ao eixo
horizontal, orientado positivamente para direita, dá o nome de eixo x ou eixo
das abscissas e ao eixo vertical, orientado positivamente para cima, dá o nome
de eixo y ou eixo das ordenadas. Ao ponto de intersecção chama de O (origem).
3 – Por fim associa, a cada um dos eixos, o conjunto de todos os números
reais. Cada ponto, de cada reta, representa um número real, sendo que o ponto
“O” (origem) vai representar o número zero, tanto em “x” quanto em “y”.
Resumindo tudo isso, ficou definido o Plano Cartesiano Ortogonal:
- Ele é constituído por dois eixos “x” e “y” perpendiculares entre si e que
se cruzam na origem (O).
- Estes eixos são orientados e associados ao conjunto de todos os números
reais, sendo que o número zero, de ambos os eixos, está exatamente na origem.
- O eixo horizontal é o eixo das abscissas e o eixo vertical é o eixo das
ordenadas.
c) Representação de pontos no Plano Cartesiano Ortogonal
Assim como representamos todos os pontos das retas dos eixos, através de cada
um dos números reais podemos, também, representar cada um dos pontos do plano
através de números.
A representação de pontos neste plano é feita através de pares ordenados,
onde o primeiro número se refere à abscissa e o segundo à ordenada, ou seja,
pares ordenados (x, y).
Assim, um determinado par ordenado (x, y) estará associado a um determinado
ponto do plano, cuja abscissa é “x” e ordenada é “y”.
Existe uma maneira geométrica para representarmos o par ordenado (x, y):
1 - desenhamos um plano cartesiano ortogonal;
2 - marcamos no eixo horizontal o ponto correspondente ao valor de “x”;
3 - marcamos no eixo vertical o ponto correspondente ao valor de “y”;
4 - traçamos por “x” uma reta paralela ao eixo vertical;
5 - traçamos por “y” uma reta paralela ao eixo horizontal;
6 - a interseção das duas retas será o ponto que representa graficamente o
par ordenado (x, y).
Exemplos:
O ponto P(3, 2) tem abscissa 3 e ordenada 2, no qual o
símbolo (3, 2) representa um par ordenado.
O ponto Q(2, 3) tem abscissa 2 e ordenada 3.
É importante frisarmos que os pontos P e Q são pontos
distintos, pois em um par ordenado a ordem dos números é relevante.
O ponto “O” da origem é representado pelo ponto O (0, 0).
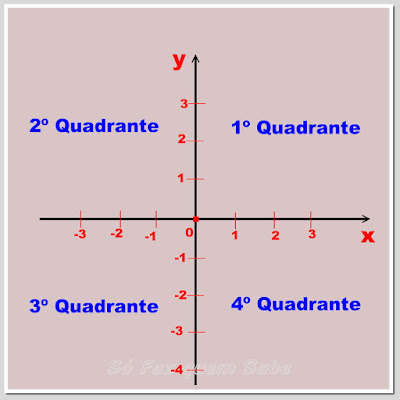
d) Quadrantes do Plano Cartesiano Ortogonal
Os dois eixos dividem o plano em quatro regiões denominadas quadrantes.
Os nomes dos quadrantes são indicados no sentido anti-horário. A região do
canto superior direito é o primeiro quadrante. A região à sua esquerda é
o segundo quadrante. Abaixo deste temos o terceiro quadrante e à
sua direita temos o quarto quadrante.
e) Sinais da Abscissa e da Ordenada de um Ponto do Plano
Todos os pontos do 1º quadrante possuem abscissa e ordenada positivas, pois
estão do lado positivo do eixo “x” e do lado positivo do eixo “Y”.
Todos os pontos do 2º quadrante possuem abscissa negativa e ordenada
positiva, pois estão do lado negativo do eixo x e do lado positivo do eixo y.
Todos os pontos do 3º quadrante têm abscissa e ordenada negativas, pois estão
do lado negativo do eixo x e do lado negativo do eixo y.
Todos os pontos do 4º quadrante têm abscissa positiva e ordenada negativa,
pois estão do lado positivo do eixo x e do lado negativo do eixo y.
Após assimilarmos os conceitos de "pares ordenados" e "plano cartesiano" temos condições de aprender "O Produto Cartesiano de Conjuntos". Acompanhem.






me ajudou muito a minha professora não sabe esplicar direito
ResponderExcluirGostei muito
ResponderExcluir