Como fazer para somar ou subtrair frações. Adição e Subtração de frações.

by Roberto M.

Hoje vamos ver como é o procedimento para somarmos duas frações ou subtrairmos uma fração de outra fração.

Já vimos o conceito de frações e sabemos que números fracionários são números que representam uma ou mais partes de uma unidade que foi dividida em partes iguais. Relembre “Frações e Números fracionários. Introduzindo o conceito.”

Ao relembrarmos os conceitos da postagem citada acima, poderemos ver que o denominador de uma fração indica em quantas partes iguais foi dividida a unidade e que o numerador de uma fração indica quantas partes iguais nós pegamos dessa unidade. Frações com denominadores diferentes indicam que a unidade foi dividida em quantidades diferentes de partes iguais.

Ora, quando vamos somar ou subtrair frações pode ocorrer uma das seguintes situações:

1ª SITUAÇÃO: As frações têm denominadores iguais

Isso significa que a unidade foi dividida no mesmo número de partes iguais e, portanto, em todas as frações as partes terão o mesmo tamanho.

Quando somamos ou subtraímos essas frações podemos, simplesmente, somar ou subtrair os numeradores (o número de partes) já que os denominadores são iguais (em quantas partes foi dividida a unidade) e continuarão os mesmos.

Vamos ver um exemplo de soma de duas frações com o mesmo denominador, vamos calcular   4/9 + 3/9

A soma de frações com denominadores iguais é uma fração cujo denominador é igual ao denominador das parcelas e cujo numerador é a soma dos numeradores das parcelas.

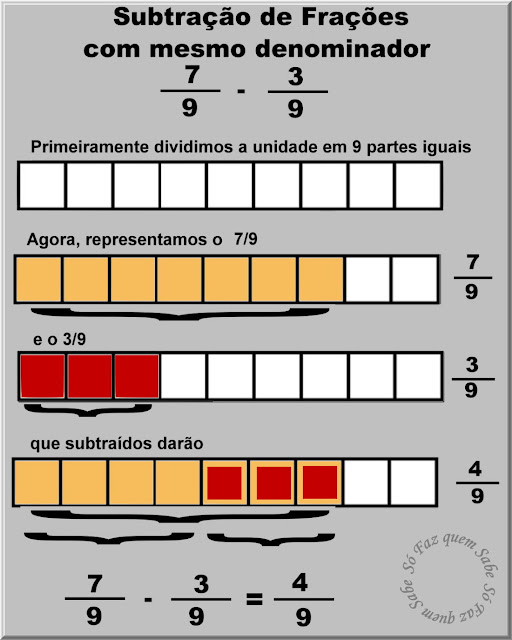
Vamos ver, agora, um exemplo de subtração de duas frações com o mesmo denominador, vamos calcular   7/9 – 3/9

A diferença entre duas frações com denominadores iguais é uma fração cujo denominador é igual ao das frações dadas e cujo numerador é a diferença entre os numeradores.

2ª SITUAÇÃO: As frações têm denominadores diferentes

Isso significa que a unidade foi dividida em em partes diferentes e, portanto, em cada uma das frações as partes terão tamanhos diferentes.

Por isso, quando formos somar ou subtrair frações com denominadores diferentes, a primeira coisa que temos que fazer é transformar cada uma das frações em frações equivalentes que tenham o mesmo denominador.
Relembre “Frações Equivalentes. Números que representam uma mesma quantidade.”

Para conseguir isso, teremos que reduzir essas frações ao mesmo denominador.
Relembre “Redução de frações a um mesmo denominador. Como fazer comparações de frações”.

Depois de reduzir as frações ao mesmo denominador, elas ficarão com denominadores iguais e, então, procederemos exatamente como na 1ª situação.

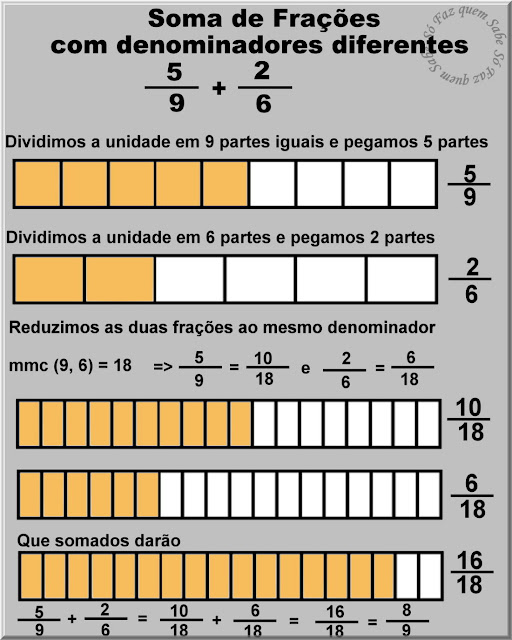
Vamos ver um exemplo de soma de duas frações com denominadores diferentes, vamos calcular   5/9 + 2/6

Quando vamos somar frações que têm denominadores diferentes, devemos primeiro reduzí-las ao mesmo denominador e, depois, aplicar as regras da 1ª situação.

Vamos ver, agora, um exemplo de subtração de duas frações com denominadores diferentes, vamos calcular   2/3 – 1/2

Quando vamos subtrair frações que têm denominadores diferentes, devemos primeiro reduzí-las ao mesmo denominador e, depois, aplicar as regras da 1ª situação.

Artigos Recomendados:

• As Quatro Operações fundamentais da Aritmética e sua nomenclatura.
• Mínimo Múltiplo Comum. Aprenda a calcular MMC.
• Frações e Números fracionários. Introduzindo o conceito.
• Tipos de Frações: próprias, impróprias e aparentes. Forma mista de um número.
• Como transformar uma fração imprópria em número misto e vice-versa.
• Como Fazer Simplificação de Frações. A forma irredutível de uma fração.