by Roberto M.
Vamos ver hoje como se faz para obter todos os divisores de um número natural qualquer. Nunca esquecendo que o 1 é divisor de qualquer número natural e que qualquer número natural, a menos do zero, é divisor dele mesmo. O zero nunca será divisor de ninguém, pois é proibido dividir por zero.
Anteriormente já aprendemos várias coisas sobre os números naturais.
Já vimos o que são números naturais (Relembre: “Conjunto dos Números Naturais. O conjunto N.“), o que são números primos ou compostos (Relembre: “Números Primos e Números Compostos. Aprenda a diferenciá-los.“) e, também, como decompor um número natural em fatores primos (Relembre: “Fatoração de um número natural.“).
Foi dada também uma noção do que vem a ser divisor e divisibilidade (Relembre: “Divisor e Divisibilidade nos números naturais.“). Lá vimos o conceito de divisibilidade e que um certo número natural a, não nulo, é divisor de um outro número natural b, quando b for divisível por a.
Por exemplo:
3 é divisor de 6, porque 6 é divisível por 3
6 é divisor de 6, porque 6 é divisível por 6
1 é divisor de 6, porque 6 é divisível por 1
CONJUNTO DOS DIVISORES DE UM NÚMERO
Vamos imaginar que precisemos descobrir, por algum motivo, quais são todos os divisores do número 12.
Para isso, podemos escrever os números de 1 a 12, examinar um a um se são ou não divisores de 12, assinalando aqueles que são.
Pois vejamos:
Pois vejamos:
1 – 2 – 3 – 4 – 5 – 6 – 7 – 8 – 9 – 10 – 11 – 12
O conjunto formado pelos números assinalados é representado por D(12) (leia D de 12). Ele é o conjunto dos divisores de 12.
D(12) = {1, 2, 3, 4, 6, 12}
O conjunto dos divisores do numero natural a é o conjunto D(a) formado por todos os números naturais que são divisores de a.
Essa é uma maneira pela qual podemos achar os divisores de um número natural mas, conforme o número vai aumentando, escrever todos os números anteriores e verificar se cada um é divisor ou não, vai ficando cada vez mais impraticável.
Então, para facilitar, vamos aprender um método prático para obter o conjunto dos divisores de um número dado, maior do que 1.
REGRA PRÁTICA PARA OBTENÇÃO DOS DIVISORES DE UM NÚMERO NATURAL
Vamos aprender fazendo um exemplo.
Vamos achar todos os divisores do número 36.
Sigamos o algoritmo (passo-a-passo) abaixo:
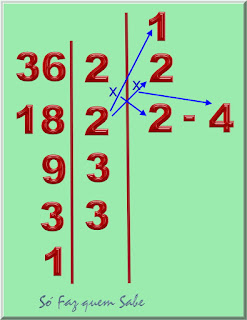
1 – Fatoramos o número dado
2 – Colocamos um traço vertical ao lado dos fatores primos
3 – Do lado direito desse traço colocamos o número 1 na linha de cima, pois o 1 é divisor de qualquer número natural
4 – Na linha do primeiro fator primo colocamos o produto dele pelo número 1 já colocado à direita do traço vertical
5 – Na linha do segundo fator primo colocamos os produtos do referido fator primo pelos números já colocados nas linhas de cima dele e à direita do traço vertical
6 - Agora, na linha de cada outro fator primo, na sequência, vamos colocando os produtos do referido fator primo pelos números já colocados nas linhas de cima dele e à direita do traço vertical
7 – As repetições são eliminadas
8 – Os números à direita do traço vertical são todos os divisores do número 36, ou seja, é o conjunto dos divisores do número 36 ou o D(36)
Artigos Recomendados:
- Reconhecendo números primos.
- Máximo divisor comum. Aprendendo a calcular MDC.
- Critérios de Divisibilidade. Verificando a divisibilidade rapidamente.
- Introdução à Teoria dos Conjuntos.
- O que são Números Primos entre Si ? Aprenda a identificar números coprimos.
- Expressões numéricas. A hierarquia das operações aritméticas e algébricas: a ordem correta das operações.







Ótimo artigo, vou compartilhar!
ResponderExcluir