sábado, 23 de novembro de 2024

Dividindo a circunferência em três partes iguais e inscrevendo um triângulo equilátero.

Passo a passo da divisão de uma circunferência em três partes iguais e consequente inscrição de um triângulo equilátero na circunferência. Aprenda essa construção geométrica.

by Roberto M.

Como fazer para construir uma circunferência dividida em três partes iguais? Como inscrever um triângulo eqüilátero numa circunferência?

Dividindo uma circunferência em três partes iguais, achamos os três vértices do triângulo equilátero inscrito nessa circunferência

Ao dividir a Circunferência em três partes iguais, acharemos os três pontos que serão os vértices do triângulo inscrito nessa circunferência.

Para aprender desenho geométrico, é aconselhável praticar. Portanto pegue lápis, régua, compasso, papel e mãos à obra.

Vamos aqui dar o passo a passo dessa construção geométrica. Vamos aprender a fazer a circundivisão em três parte iguais e a consequente inscrição do triângulo equilátero correspondente.

Passo 1

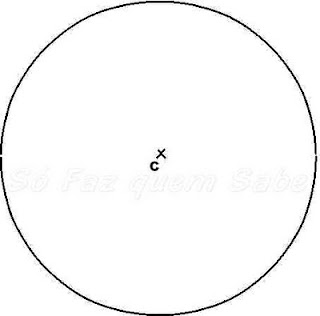
Marque no papel um ponto C. Pegue o compasso e com a ponta seca no ponto C, trace uma circunferência com o raio que desejar.

Com centro no ponto C, traçar uma circunferência

Passo 2

Pegue uma régua e trace um diâmetro da circunferência, marcando os pontos A e B. Não se esqueça, diâmetro é o segmento de reta que une dois pontos da circunferência passando pelo centro C.

Passo 3

Pegue o compasso novamente, abra-o com uma abertura igual ao raio da circunferência que você traçou, ou seja, medida da abertura igual a AC ou BC. Com centro em B (coloque a ponta seca do compasso no ponto B), trace um arco que intersecte a circunferência em dois pontos D e E.

Traçar um arco que intersecte a circunferência nos pontos D e E. A, D e E dividem a circunferência em três arcos iguais

Passo 4

Pronto, os pontos A, D e E dividem a circunferência em três partes iguais, ou seja, os arcos AE, ED e DA são congruentes (tem a mesma medida). Como esses arcos são congruentes, as cordas AE, ED e DA da circunferência, também são congruentes. Logo, os pontos A, D e E são os vértices de um triângulo eqüilátero (os três lados com medidas iguais).

Portanto, ao pegar o lápis e a régua e unir o ponto A ao ponto E; o ponto E ao ponto D e o ponto D ao ponto A você estará desenhando o triângulo equilátero inscrito na circunferência.