by Roberto M.
O que são ângulos consecutivos? E ângulos adjacentes? Quais são os ângulos retos, agudos e obtusos? O que significa ângulo raso ou de meia volta? O que é um ângulo nulo e ângulo de uma volta?
Agora que já sabemos o que é ângulo e qual a unidade utilizada para medi-lo, podemos nos aprofundar mais um pouco e definir seus elementos e classificação.
A essa origem comum chamamos vértice do ângulo. Às semi-retas chamamos lados do ângulo.
ÂNGULO NULO E DE UMA VOLTA
Quando as semi-retas de mesma origem coincidem, temos o ângulo nulo e o ângulo de uma volta.
O ângulo nulo é formado apenas pelas semi-retas coincidentes e mede zero grau (0°)
ÂNGULO RASO OU DE MEIA VOLTA
Quando as semi-retas de mesma origem não são coincidentes, mas estão contidas na mesma reta, temos o ângulo raso ou de meia volta.
O ângulo raso ocupa meio plano e mede 180 graus (180°).
ÂNGULOS CONSECUTIVOS
Dizemos que dois ângulos são consecutivos quando possuem o mesmo vértice e um lado comum.
Observe a figura abaixo:
Nela identificamos os ângulos AÔC, CÔB E AÔB.
Os ângulos AÔC e CÔB possuem vértice comum (O) e lado comum (OC).
Os ângulos AÔC e AÔB possuem vértice comum (O) e lado comum (AO).
Os ângulos CÔB e AÔB possuem vértice comum (O) e lado comum (OB).
Os pares de ângulos AÔC e CÔB, AÔC e AÔB, CÔB E AÔB são denominados ângulos consecutivos por terem o mesmo vértice e um lado comum.
ÂNGULOS ADJACENTES
Dizemos que dois ângulos são adjacentes quando são consecutivos e não possuem pontos internos comuns
Observe a figura abaixo:
Nela identificamos os ângulos AÔC, CÔB E AÔB.
Os ângulos AÔC e CÔB são consecutivos e não possuem pontos internos comuns e, por isso, são ângulos adjacentes.
Já os ângulos AÔC e AÔB e os ângulos CÔB e AÔB são consecutivos, mas possuem pontos internos comuns e, por isso, não são ângulos adjacentes.
CLASSIFICAÇÃO EM RETO, AGUDO E OBTUSO.
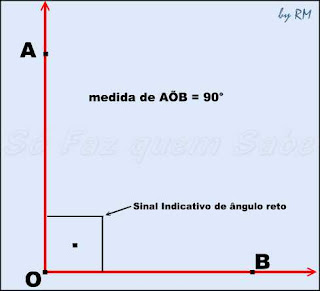
Ângulo Reto é o ângulo cuja medida é 90 graus (90°).
Ângulo Agudo é o ângulo cuja medida é menor que 90 graus (90°).
Ângulo Obtuso é o ângulo cuja medida é maior que 90 graus (90°).
ÂNGULOS COMPLEMENTARES
Dois ângulos são complementares quando a soma de suas medidas é 90 graus (90°).
Observe a figura abaixo, onde o ângulo AÔB mede 90°:
Verifique que a medida do ângulo AÔC mais a medida do ângulo CÔB é igual a 90 graus, ou seja: m(AÔC) + m(CÔB) = 90°.
Por isso, diz-se que os ângulos AÔC e CÔB são complementares.
Exemplo:
Os ângulos 35° e 55° são complementares, pois 35° + 55° = 90°.
Dizemos que o ângulo de 35° é o complemento do ângulo de 55°, e vice-versa.
Para calcular a medida do complemento de um ângulo, devemos determinar a diferença entre 90° e a medida do ângulo dado.
Se a medida do ângulo for (x), seu complemento será (90° - x).
ÂNGULOS SUPLEMENTARES
Dois ângulos são suplementares quando a soma de suas medidas é 180 graus (180°).
Observe a figura abaixo, onde o ângulo AÔB é um ângulo raso e mede 180°:
Verifique que a medida do ângulo AÔC mais a medida do ângulo CÔB é igual a 180 graus, ou seja: m(AÔC) + m(CÔB) = 180°.
Por isso, diz-se que os ângulos AÔC e CÔB são suplementares.
Exemplo:
Os ângulos 60° e 120° são suplementares, pois 60° + 120° = 180°.
Dizemos que o ângulo de 60° é o suplemento do ângulo de 120°, e vice-versa.
Para calcular a medida do suplemento de um ângulo, devemos determinar a diferença entre 180° e a medida do ângulo dado.
Se a medida do ângulo for (x), seu suplemento será (180° - x).










Tem um erro na matéria, repare na definição de angulos adjacentes, primeiro é falado que AÔB e AÔC é adjacente, depois, na linha seguinte é dito que ele não é adjacente... Como que é isso?
ResponderExcluirÔpa! Foi um erro de digitação. Tinha trocado o C pelo A.
ExcluirObrigado caro desconhecido por me ajudar a detectá-lo.
Já está corrigido.
O que seria o conceito de "ponto interno em comum" ? Não me parece muito intuitivo.
ExcluirConsideramos "pontos internos", todos aqueles pontos que estão internamente delimitados pelos lados do ângulo, excluindo-se os pontos que formam os próprios lados. Falando de um modo mais simples: são os pontos que estão dentro do ângulo e não considerando os pontos dos lados.
Excluir"Pontos internos em comum" seriam os pontos internos que pertencem a dois ângulos ao mesmo tempo.
Note que no conceito de ângulos adjacentes, os únicos pontos em comum são os pontos de um dos lados, não tendo nenhum ponto considerado interno que pertence aos dois ângulos ao mesmo tempo.