by Roberto M.
Como se faz para dividir uma circunferência em seis partes iguais?
Qual é o método que se utiliza para inscrever um hexágono numa circunferência?
Como se faz para construir um hexágono regular?
Já vimos no artigo “Polígono. Classificação e Nomenclatura” que hexágono é um polígono de seis lados. Vimos também, que hexágono regular é o polígono de seis lados que tem todos os lados iguais.
Portanto, quando dividimos uma circunferência em seis partes iguais, os seis pontos que achamos são também os vértices do hexágono regular inscrito na circunferência.
Vamos, então, pegar lápis, papel, régua e compasso para aprender a fazer essa construção geométrica. Sigamos os passos abaixo:
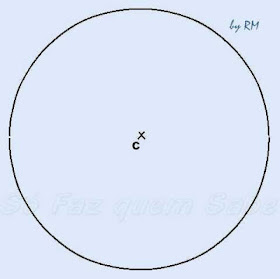
PASSO 1
Primeiramente
vamos traçar uma circunferência. Marcamos um ponto C no papel e,
com o compasso aberto com um raio qualquer, traçamos uma circunferência com
centro no ponto C.
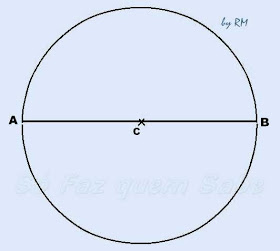
PASSO 2
Com a
régua, traçamos um diâmetro qualquer da circunferência e marcamos os
pontos A e B.
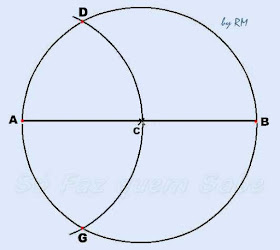
PASSO 3
Em
seguida, pegamos o compasso com a mesma abertura que fizemos a circunferência,
ou seja, com o mesmo raio da circunferência e, com centro no ponto A
traçamos um arco que intersecte a circunferência nos pontos D
e G.
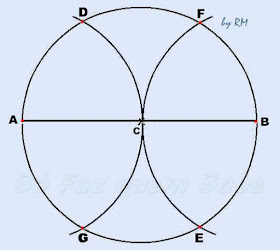
PASSO 4
Ainda
com o compasso e com a mesma abertura, agora com centro em B, traçamos um arco
que intersecte a circunferência nos pontos E
e F.
PASSO 5
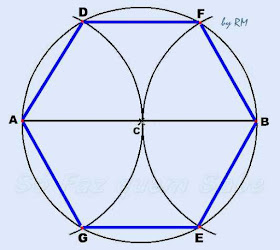
Os
pontos A, D, F, B, E,
e G dividem a circunferência em seis
arcos iguais e, por isso, são, também, os vértices do hexágono regular inscrito
nessa circunferência.
Ao
uni-los, estaremos construindo o hexágono regular que desejávamos.
Podemos observar que a medida do lado do hexágono regular inscrito na circunferência é exatamente igual à medida do raio dessa mesma circunferência.

bom
ResponderExcluirObrigado.Me ajudou muito eu estou tendo aulas online e já não me lembrava como fazer e este site me ajudou muito.
ResponderExcluirMe ajudou muito
ResponderExcluirMuito bem feito
ResponderExcluirMuito obrigado! Foi muito proveitoso 🙏🙏🙏🙏
ResponderExcluir