by Roberto M.
Outro dia, ensinei a fazer uma estrela de seis pontas devido à necessidade
de minha esposa, que é professora de artes manuais, para um dos projetos de patchwork com seus alunos. A necessidade dela não parou por aí. Em outro trabalho ela precisou de um
molde para uma estrela de cinco pontas.
Descobri, então, que de vez em quando também é necessário saber desenhar,
geometricamente, um polígono estrelado de cinco pontas.
Por isso, resolvi mostrar como é a construção geométrica de uma estrela de
cinco pontas.Para isso, necessitaremos de papel, lápis, régua e compasso.
Primeiramente, devemos dividir uma circunferência em cinco partes
iguais para, depois, traçarmos as linhas que formarão a estrela.
Vamos ao passo a passo da construção geométrica de um polígono
estrelado de cinco pontas:
Passo 1
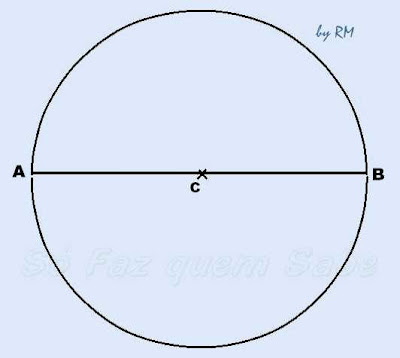
Primeiramente, devemos traçar, no papel e com o compasso, uma circunferência
do tamanho que desejamos a nossa estrela.
Passo 2
Com a régua, traçamos um diâmetro qualquer da circunferência e
marcamos os pontos A e B.
Passo 3
Pegamos o compasso com uma abertura maior do que o raio da circunferência
traçada e, com centro no ponto A e no ponto B, traçamos dois arcos
que se intersectem no ponto D. Ele servirá para traçarmos a
perpendicular, passando pelo centro, ao diâmetro marcado anteriormente e
encontrarmos o ponto E.
Quem quiser relembrar como se faz para traçar retas perpendiculares leia o
artigo “Retas perpendiculares que se cruzam num ponto
dado”.
Passo 4
Agora, vamos seguir os passos do artigo “Divisão da circunferência em cinco partes iguais.
Construindo um pentágono regular.” até dividir a circunferência em
cinco partes iguais.
Primeiramente, utilizando o que aprendemos no artigo "Mediatriz e ponto médio de um segmento" vamos
obter o ponto M, ponto médio do raio BC.
Pegamos o compasso, e com centro em B e C traçamos os arcos acima e abaixo do
segmento BC achando os pontos G e H que determinarão a mediatriz e
consequentemente o ponto médio M do raio BC.
Depois, com centro no ponto M e com uma abertura do compasso até o ponto E,
descreve-se um arco até o diâmetro horizontal AB determinando o ponto P.
Passo 5
A distância do ponto E ao ponto P é a medida da corda correspondente ao arco
que é a quinta parte da circunferência.
Fazendo-se centro em E, transporta-se a distância EP para a circunferência e
obtém-se o ponto 1.
A partir do ponto 1, marca-se mais três vezes este comprimento (1E) e
determina-se os pontos 2, 3 e 4.
Passo 6
Pronto!
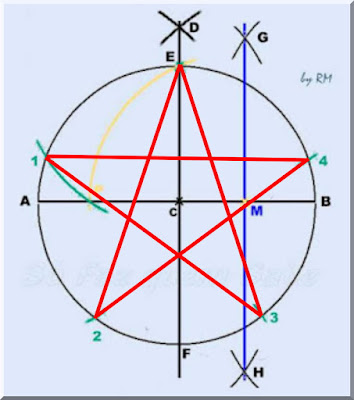
Os pontos 1, 2, 3, 4 e E dividem a circunferência em cinco arcos
iguais e, por isso, são, também, as pontas da nossa estrela.
Basta, agora, traçarmos os segmentos 1 4, 4 2, 2 E, E 3 e 3 1, que teremos inscrito na circunferência nosso polígono estrelado de 5
pontas.
Artigos Recomentados:
- Como dividir uma circunferência em 3 partes iguais e inscrever um triângulo
- Divisão da circunferência em quatro partes iguais
- Construção do Heptágono regular. Dividindo a circunferência em sete partes iguais.
- Octógono Regular e a circunferência dividida em oito partes iguais.
- Nomeando os polígonos. Classificação dos polígonos quanto ao número de lados.





Obrigada! Foi de grande utilidade. Fiz minha estrela e ficou linda.
ResponderExcluirMuito bom
ResponderExcluirmuito obrigado me ajudou muito
ResponderExcluirMe fez lembrar muitas coisas de geometria. Foi muito útil. Obrigada.
ResponderExcluirExcelente ajudou demais! Foi bom recordar! Obrigado!
ResponderExcluirobrigada, bastante esclarecedor.
ResponderExcluir