by Roberto M.
Quando vamos medir a distância entre dois pontos usamos as unidades de comprimento. Já estudamos o “Metro, a unidade padrão de comprimento”, vale a pena relembrar.
Vimos, também, como trabalhar com essas medidas de comprimento, quando estudamos “Unidades de comprimento no sistema métrico decimal. Fazendo as conversões”. Relembre também.
Hoje vamos ver como medir uma superfície.
Sabemos, intuitivamente, o que é uma superfície, e que ela é uma grandeza com duas dimensões. A área é a medida dessa grandeza.
Mas o que é grandeza? Grandeza é tudo aquilo que pode ser medido.
E o que é medir? É associar valores numéricos às grandezas, comparando esses valores com um valor padrão denominado unidade de medida.
Primeiramente, vamos entender melhor o que significa medir uma superfície:
ÁREA DE UMA SUPERFÍCIE
Abaixo, veremos algumas regiões ou superfícies planas. São curvas fechadas simples reunidas com o conjunto de pontos internos a elas (relembre o que é isso vendo: “Diferenças entre linha, curva e poligonal. Regiões geométricas”).
Medir uma superfície significa comparar essa superfície com outra superfície tomada como unidade padrão e estabelecer quantas vezes a unidade cabe na superfície dada.
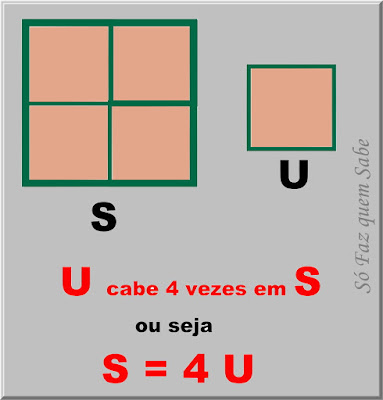
Vamos ver alguns exemplos, onde uma superfície que chamaremos de S está sendo comparada com a unidade chamada U.
Exemplo 1
Exemplo 2
O número de vezes que a unidade de superfície U cabe numa determinada superfície S é chamado de medida da superfície S ou Área da superfície S.
Portanto, nos exemplos acima, podemos dizer que a área da superfície S vale 4 ou 9, respectivamente.
UNIDADE DE ÁREA
Conforme visto nos exemplos acima, qualquer superfície pode ser escolhida como unidade de área.
Se qualquer pessoa pudesse escolher livremente uma unidade de área, provavelmente, cada uma escolheria uma unidade diferente. Desse modo, a mesma superfície S poderia apresentar diversas medidas, dependendo da unidade utilizada.
É por isso, que existe a necessidade de se utilizar uma unidade padrão, ou seja, uma unidade de forma e tamanho conhecidos e que seja aceita e utilizada por todas as pessoas.
A unidade padrão escolhida e aceita por todo o mundo é o metro quadrado ( m2 ).
O metro quadrado corresponde à medida de uma superfície de um quadrado de 1 metro de lado.
A figura acima é uma tentativa de representação do que é um metro quadrado.
MÚLTIPLOS E SUBMÚLTIPLOS DO METRO QUADRADO
O metro quadrado é a unidade fundamental para medir superfícies. Entretanto, dependendo do tamanho da superfície a medir, a unidade metro quadrado se torna pouco prática.
Se a superfície for muito grande, teremos de usar muitos algarismos para representá-la em metros quadrados; se a superfície for muito pequena, a unidade metro quadrado acaba se tornando grande demais e a representação da medida fica sem precisão.
Para acabar com esse problema, foram criadas as unidades secundárias de área, ou seja, os múltiplos e submúltiplos do metro quadrado.
Se quisermos medir grandes superfícies, como por exemplo a área de um país, empregamos como unidade um dos múltiplos do metro quadrado. Se quisermos medir pequenas superfícies, como por exemplo a área de uma moeda, empregamos como unidade um dos submúltiplos do metro quadrado.
múltiplos do metro quadrado:
A figura acima tenta mostrar o fato de que um decâmetro quadrado é igual a cem metros quadrados.
- decâmetro quadrado: cujo símbolo é dam2 e vale:
1dam x 1dam = 10m x 10m =
1dam2 = 100m2
- hectômetro quadrado: cujo símbolo é hm2 e vale:
1hm x 1hm = 10dam x 10dam = 100m x 100m =
1hm2 = 100dam2 = 10 000m2
- quilômetro quadrado: cujo símbolo é km2 e vale:
1km x 1km = 10hm x 10hm = 100dam x 100dam = 1000m x 1000m =
1km2 = 100hm2 = 10 000dam2 = 1 000 000m2
submúltiplos do metro quadrado:
A foto acima tenta mostrar que um metro quadrado é igual cem decímetros quadrados.
- decímetro quadrado: cujo símbolo é dm2 e vale:
1m2 = 1m x 1m = 10dm x 10dm = 100dm2
1dm2 = 1/100m2 = 0,01m2
- centímetro quadrado: cujo símbolo é cm2 e vale:
1m2 = 1m x 1m = 10dm x 10dm = 100cm x 100cm = 10000cm2
1cm2 = 1/10 000m2 = 0,0001m2
- milímetro quadrado: cujo símbolo é mm2 e vale:
1m2 = 1m x 1m = 10dm x 10dm = 100cm x 100cm = 1000mm x 1000mm = 1000000 mm2
1mm2 = 1/1 000 000mm2 = 0,000001mm2
Observando as informações acima, podemos notar que cada múltiplo é 100 vezes maior que o múltiplo anterior e cada submúltiplo é 100 vezes menor que o submúltiplo anterior. Veja a tabela:
Múltiplos
|
Unidade Fundamental
|
Submúltiplos
| ||||
quilômetro quadrado
|
hectômetro quadrado
|
decâmetro quadrado
|
metro quadrado
|
decímetro quadrado
|
centímetro quadrado
|
milímetro quadrado
|
km2
|
hm2
|
dam2
|
m2
|
dm2
|
cm2
|
mm2
|
1 000 000
(m2)
106
|
10 000
( m2)
104
|
100
(m2)
102
|
1
(m2)
|
0,01
(m2)
10-2
|
0,001
(m2)
10-4
|
0,000001
(m2)
10-6
|
Portanto, a casa da esquerda é sempre 100 vezes maior que a sua vizinha da direita e a casa da direita é sempre 100 vezes menor que a sua vizinha da esquerda.
Sendo assim, a área de uma superfície qualquer terá uma representação numérica diferente, dependendo da unidade que se usar.
Exemplo
Vamos a um exemplo para ilustrar: Um bairro que tem 1 km2 de área terá:
- 1 km2
- 100 hm2, pois cada km2 tem 100 hm2
- 10 000 dam2, pois cada hm2 tem 100 dam2
- 1 000 000 m2, pois cada dam2 tem 100 m2
- 100 000 000 dm2, pois cada m2 tem 100 dm2
- 10 000 000 000 cm2, pois cada dm2 tem 100 cm2
- 1 000 000 000 000 mm2, pois cada cm2 tem 100 mm2
CONVERSÃO DAS UNIDADES DE ÁREA
Analisando atentamente o exemplo acima, podemos notar o seguinte:
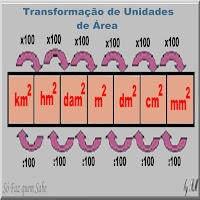
1- Para passar de uma unidade, para outra imediatamente á direita na tabela, devemos fazer uma multiplicação por 100.
2- Para passar de uma unidade, para outra imediatamente à esquerda na tabela, devemos fazer uma divisão por 100.
3- Para passar de uma unidade, para outra qualquer que não seja vizinha, devemos aplicar as regras anteriores sucessivas vezes.
3- Para passar de uma unidade, para outra qualquer que não seja vizinha, devemos aplicar as regras anteriores sucessivas vezes.
Veja o esquema abaixo:
Portanto, para fazer as conversões, basta seguir o esquema acima.
Lembrando que na numeração decimal, para multiplicar um número por 100, é só deslocar a vírgula duas casas para a direita e para dividir por 100 é só deslocar a vírgula duas casas para a esquerda.
Lembrando que na numeração decimal, para multiplicar um número por 100, é só deslocar a vírgula duas casas para a direita e para dividir por 100 é só deslocar a vírgula duas casas para a esquerda.
Para fixar, vamos a alguns exemplos:
1- Passar 18, 347568 hm2 para metro quadrado
Pelo esquema, verificamos que de hm2 para m2 temos que “andar” quatro casas para a direita. Portanto, temos que multiplicar por 100 e depois por 100 novamente, ou seja, deslocar a vírgula quatro casas para a direita.
18, 347568 hm2 = 183475,68 m2
2- Converter 233568, 432 cm2 para decâmetro quadrado
Pelo esquema verificamos que de cm2 para dam2 temos que “andar” seis casas para a esquerda. Portanto, temos que dividir por 100, por 100 novamente e uma terceira vez dividir por 100, ou seja, deslocar a vírgula seis casas para a esquerda.
233568, 432 cm2 = 0, 233568432 dam2
Como podemos ver, fazer a conversão de unidade de área é muito simples. Basta fazer o esquema dos múltiplos e submúltiplos (conforme o modelo acima), contar as casas que se quer “andar” e mudar a vírgula do número, para a direita ou esquerda conforme o caso.






Nenhum comentário:
Postar um comentário