by Roberto M.
Já falamos, em outras postagens, da importância dos símbolos na matemática. Quase tudo na matemática gira em torno de símbolos. Desde os próprios algarismos, que expressam quantidades, até os sinais de adição, subtração, multiplicação e divisão.
Alguns símbolos explicitam operações simples e outros são usados para compactar operações mais complexas e as tornar mais simples de visualizar no papel.
Como exemplos desses últimos, temos a notação dos somatórios definidos que serve para compactar a visualização da soma de um certo número de parcelas previamente definidas (Veja: A Notação Sigma. Um símbolo para os somatórios definidos.) e a notação fatorial, que serve para compactar a visualização do produto de todos os números naturais inferiores ou iguais a um certo número dado (Veja: A Notação Fatorial - n! – O que é, e como calcular um fatorial).
Hoje vamos falar sobre um outro símbolo muito usado na matemática, principalmente nos processos em que se exigem cálculos do produto de um conjunto de números.
Assim como existe o símbolo para o somatório, existe também um símbolo para o produtório.
Para denotar um produto de vários números, usa-se a letra maiúscula grega PI (P).
O PI (P) é o “pê (p)” em grego e significa “produtório definido” de vários números na matemática. Essa notação é usada para abreviar a indicação de grandes produtos.
Assim, se uma variável “y” tiver os valores 3, 6, 7 e 8 poderemos expressar o produto dessas variáveis da seguinte maneira:
3 x 6 x 7 x 8 = Py
A notação produtório é útil, mas é pouco usada em comparação à notação somatório.
Mas, vamos generalizar a convenção dessa tal “notação PI”, a notação produtório:
NOTAÇÃO PRODUTÓRIO DEFINIDO (UTILIZANDO A LETRA GREGA PI MAÍUSCULA)
Dada uma sucessão de números reais (y1, y2, y3, y4, y5, ..., yn) representa-se o seu produto por:
A leitura dessa notação se faz da seguinte maneira:
Produtório dos valores da variável (y) começando do primeiro (i=1) e terminando no enésimo (i=n).
Note-se que podemos definir o que quisermos de acordo com nossa necessidade. Assim, podemos dizer que o (i) varia do primeiro ao quinto, ou do terceiro ao sétimo, etc.
EXEMPLOS
1°) Produtório dos 5 primeiros elementos de um conjunto.
2°) Multiplicar os elementos de um conjunto que estão entre o terceiro e o sétimo, inclusive eles.
Isso significa que devemos fazer o produto dos valores da variável (y) começando com o terceiro (i=3) e terminando com o sétimo (i=7).
3°) Se apenas uma parte dos valores das variáveis é que deve ser multiplicada, usamos os índices, como indicados acima, para determinar a parte que queremos multiplicar. No entanto, se quisermos multiplicar a totalidade dos valores das variáveis de um conjunto, ou seja, multiplicar todas as observações; costuma-se escrever a notação abreviadamente, sem os índices.
UTILIZAÇÃO DO PRODUTÓRIO
A notação produtório (P) é utilizada para representar, numa forma reduzida, uma expressão, números, funções, etc., colocados em certa ordem e separados por sinal de produto (X)⋅.
EXEMPLOS
1°) Produtório de yi com i variando de 3 a 7
2°) Produtório de (2i + 1) com i variando de 1 a 4
PROPRIEDADES DO PRODUTÓRIO
1°) Produtório de uma constante
O produtório de uma constante (isto é, o produto de uma constante n vezes) é igual à constante elevada ao número n. Ou seja:
2°) Distributiva em relação ao produto
O produtório de um produto de duas variáveis é igual ao produto dos produtórios individuais. Ou seja:
3°) Produtório de uma variável multiplicada por uma constante
Em um produtório de n elementos, quando cada valor de uma variável deve ser multiplicado por uma constante, essa constante elevada ao número n pode ser aplicada ao produtório das variáveis. Ou seja:
4°) Produtório de uma variável elevada a uma constante
O produtório de (uma variável elevada a uma constante) é igual ao (produtório da variável) elevado à constante. Ou seja:
CURIOSIDADE
Como vimos na postagem “A Notação Fatorial - n! – O que é, e como calcular um fatorial”, fatorial é “o produto de todos os números naturais inferiores ou iguais a um certo número dado. Portanto, o fatorial de um número n nada mais é que o produtório de todos os números naturais inferiores ou igual a esse número n. Ou seja:
Como podemos ver, todo fatorial é um produtório mas, nem todo produtório é fatorial.
EXERCÍCIOS COM PRODUTÓRIO
1°) Simplifique a expressão
2°) Escreva a expressão usando a notação de produtório
Artigos Recomendados:
- Expressões numéricas. A hierarquia das operações aritméticas e algébricas: a ordem correta das operações.
- As Quatro Operações fundamentais da Aritmética e sua nomenclatura.
- Algarismos Significativos. Números exatos e não exatos.
- A Notação Científica. Representando valores, de forma padronizada, com potências de base 10.
- O que são Números Primos entre Si ? Aprenda a identificar números coprimos.
- Fatoração de um número natural.

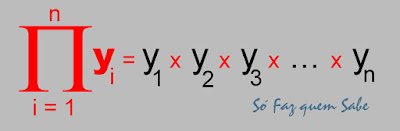












Nenhum comentário:
Postar um comentário