by Roberto M.
Outro dia falamos sobre as Dízimas Periódicas, hoje falaremos sobre as Dízimas Não Periódicas.
Dízimas Não Periódicas são um tipo de decimal muito curioso. Eles possuem uma parte decimal que, além de ser infinita, não se repete periodicamente.
Uma Dízima Não Periódica é um tipo de número que tem infinitas casas depois da vírgula, mas esses algarismos depois da vírgula não se repetem em um padrão regular, diferentemente das dízimas periódicas, que têm um padrão onde um grupo de algarismos se repetem indefinidamente.
Ao contrário da dízima periódica, a Dízima Não periódica não segue um ciclo previsível dos seus algarismos após a vírgula. Isso faz com que os seus dígitos continuem infinitamente sem se repetir em um padrão específico.
É importante frisar que a Dízima Não Periódica não consegue ser representada como fração de dois números inteiros e portanto nunca será um número racional.
As Dízimas Não Periódicas não possuem representação fracionária, ao contrário das dízimas periódicas.
Uma das propriedades mais curiosas das dízimas não periódicas é a sua natureza aparentemente caótica e imprevisível .
Ao contrário das dízimas periódicas, que seguem um padrão regular de repetição, as Dízimas Não Periódicas parecem desafiar qualquer tipo de regularidade ou lógica.
Que fique bem claro: Todos os números decimais com infinitas casas depois da vírgula que não seguem um padrão regular de repetição são Dízimas não Periódicas.
Para se conseguir uma Dízima Não Periódica, basta criar um número decimal infinito que não se repita periodicamente. Entretanto, existem várias Dízimas Não Periódicas ‘famosas’, muito conhecidas, com as quais temos contato a todo momento. Vamos ver alguns exemplos:
EXEMPLOS DE DÍZIMAS NÃO PERIÓDICAS
1) Raízes não exatas - Quando um número natural não possui raiz exata, se formos procurar a resposta para a radiciação, encontraremos uma Dízima Não Periódica, números com infinitas casas decimais não periódicas.
Ao resolver-se essas raízes, a resposta sempre vai ser uma aproximação, o que chamamos de Dízimas Não Periódicas.
2) Número π (PI): é bastante comum nos cálculos envolvendo curvas. O número π (PI) é uma constante matemática que representa a relação entre o diâmetro e o perímetro de uma circunferência . É uma das mais conhecidas Dízimas Não Periódicas.
Pelo fato de ser irracional, utilizamos um símbolo para representá-lo. Seu valor é igual a 3,14159265358979323846…
São conhecidas 62,8 trilhões de casas decimais desse número, mas normalmente utilizamos uma aproximação, com o valor de 3,14.
3) Número j (FI): é conhecido também como número de ouro ou proporção áurea e é estudado desde a Antiguidade. A proporção áurea é um conceito matemático que surge quando uma linha é dividida em duas partes de forma a obter-se uma razão especial entre os dois comprimentos, sendo essa razão o número j(FI).
Descreve vários fenômenos da natureza e há também relatos do uso dessa proporção em obras artísticas. É um número irracional, e por isso é representado pelo símbolo j, sendo seu valor igual a 1,61803398875…
4) Número (e) ou Constante de Euler: Alternativamente, o número (e) pode ser chamado de constante Neperiana, ou de Neper. Essa constante é utilizada, principalmente, em assuntos da matemática financeira.
Na matemática tradicional, é a base dos logaritmos naturais. Por ser um número irracional, é representada pelo símbolo e, sendo seu valor igual a 2,718281828459045235360…
Vejam que, em todos esses exemplos, a parte decimal é infinita e que não existe um período, ou seja, uma sequência que faça com que consigamos prever o próximo número da parte decimal. É por isso que chamamos todos esses números de Dízimas Não Periódicas.


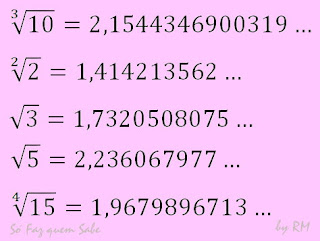



Nenhum comentário:
Postar um comentário