Qual é o conceito de ângulo? O que é um ângulo? Qual é a unidade de medida de um ângulo?
A partir das noções fundamentais da geometria, onde tivemos a ideia de ponto, reta e plano, pudemos avançar nos conceitos e entender o que é segmento de reta e semi-reta.
Sabendo o que é semi-reta, podemos conceituar ângulo da seguinte maneira:
Vamos tentar explicar melhor exemplificando.
Observe a figura abaixo:
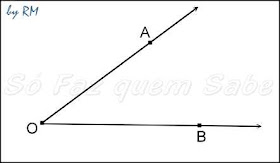
Na figura vemos duas semi-retas: a semi-reta OA e a semi-reta OB.
As duas semi-retas são distintas.
O ponto O é origem das duas semi-retas.
Essas duas semi-retas (OA e OB) de mesma origem formam um ângulo, ao qual chamamos ângulo AÔB.
Na realidade, o ângulo AÔB é a união das duas semi-retas distintas e de mesma origem.
Ao ponto O, origem das duas semi-retas, chamamos vértice do ângulo.
Às semi-retas OA e OB chamamos lados do ângulo.
MEDIDA DOS ÂNGULOS
Agora que sabemos o que é um ângulo, temos que saber como medi-los.
Para entender melhor a história da medida de um ângulo, leia o artigo “Por que a circunferência mede 360 graus? ”. Ali descobriremos como surgiu a unidade de medida dos ângulos, unidade essa que se chama grau.
Mas para resumir, podemos dizer que a unidade de medida de um ângulo surgiu lá pelos anos 150 a.C.
Nessa época, um famoso matemático chamado Hiparco de Nicéia resolveu dividir a circunferência em partes iguais e a dividiu em 360 partes. A cada uma dessas partes deu o nome de arco de um grau (1°) e a circunferência por ter 360 arcos de um grau acabou ficando com 360°.
A partir daí, acabou sendo definido o ângulo de um grau (1°) como sendo o ângulo que determina um arco de 1° em qualquer circunferência cujo centro seja o vértice desse ângulo. Veja a figura:
Definido o ângulo de 1°, todos os outros ângulos estão com suas medidas garantidas. Basta compará-los à medida do arco de 1°, ou seja, a 1/360 (um trezentos e sessenta avos) de qualquer circunferência cujo centro seja o vértice desse ângulo. (Não se esqueça, leia o artigo “Por que a circunferência mede 360 graus?”).
Por exemplo, ângulo de 90° é o ângulo que determina um arco de 90° em qualquer circunferência cujo centro seja o vértice desse ângulo. Veja a figura:
Sempre é bom lembrar, que a unidade grau não é base 10 (decimal) e sim base 60.
Como é base 60, cada 1 grau é dividido em 60 partes iguais e cada uma dessas partes recebe o nome de um minuto (1’).
Cada 1 minuto (1’) também é dividido em 60 partes iguais e cada uma dessas partes recebe o nome de 1 segundo (1’’).



Nenhum comentário:
Postar um comentário