by Roberto M.
A matemática, às vezes, nos prega algumas peças que parecem não ter explicação. Entretanto, se analisarmos, com critério, todas as passagens e, à luz das regras algébricas corretas, sem dúvida e com certeza, conseguiremos desvendar o mistério.
Devemos ficar atentos: há coisas na matemática que nunca, em hipótese alguma, podemos fazer. Existem regras, que se descumpridas, levam a incoerências inimagináveis.
Hoje iremos provar que: 2 = 1
Mas espere, 2 é igual a 1 ?
Vamos provar que sim:
1 - Primeiramente vamos considerar dois números pertencentes ao conjunto dos números reais: X e Y diferentes de zero.
Vamos supor que X seja igual a Y e a partir disso desenvolver nossa demonstração.
2 - Quando multiplicamos os dois lados de uma igualdade pelo mesmo número, a igualdade não se modifica. Então vamos multiplicar os dois lados da igualdade por X e teremos: X X = Y X ou seja X2 = YX
3 - Quando somamos ou subtraímos o mesmo número de ambos os lados da igualdade, ela também não se modifica. Então vamos subtrair de ambos os lados da igualdade o número Y2 e teremos: X2 – Y2 = YX - Y2
4 - Quem se lembra da fatoração da “Diferença de dois Quadrados”? Pois é, por ela sabemos que X2–Y2 = (X+Y) (X–Y) então, teremos: (X+Y) (X–Y) = YX–Y2
5 - Se fatorarmos o lado direito da igualdade colocando o Y em evidência teremos:
(X + Y) (X – Y) = Y (X – Y)
(X + Y) (X – Y) = Y (X – Y)
6 - Se dividirmos ambos os lados por (X – Y) teremos: (X + Y) = Y
7 - Como por nossa suposição inicial X = Y, podemos substituir X por Y e então teremos: (Y + Y) = Y Que dará: 2Y = Y
8 - Dividindo-se ambos os lados por Y concluiremos que: 2 = 1
É claro que essa demonstração possui um erro muito grave. Nem é preciso entender muito de matemática para saber que 2 não é igual a 1.
Vamos tentar descobrir onde está o erro dessa demonstração sem olhar a resposta.
Se alguém não conseguir desvendar o mistério de maneira alguma, daí sim …
Clique no botão abaixo para descobrir qual é o erro:
*********************************************
Explicando o erro da demonstração do 2 = 1
No item 5 de nossa demonstração, chegamos a um ponto onde temos:
(X + Y) (X – Y) = Y (X – Y)
Na próxima etapa da nossa demonstração, no item 6, dividimos ambos os lados por:
(X – Y)
Bingo!! Aí está o erro!
Em princípio, dividir ambos os lados de uma igualdade por um mesmo número não altera a igualdade.
Mas…
Nossa suposição inicial era que X = Y
Portanto temos que X – Y = 0
E o principal mandamento da Matemática nos diz:
“Nunca, jamais, em hipótese alguma, dividirás por zero”
Esse é o maior pecado matemático que pode existir. Cometer esse pecado significa chegar a conclusões ilógicas, incoerentes, disparatadas, despropositadas, incongruentes, contraditórias, insensatas, malucas, fantásticas, ridículas ou quantos mais sinônimos a palavra absurdo possa ter.
*********************************************
Artigos Recomendados:
- Processo para extrair a Raiz Quadrada de um número na Raça.
- Como fazer arredondamento da numeração decimal.
- Conversão de Números Binários em Decimais
- Fatoração de um número natural.
- O que são Números Primos entre Si ? Aprenda a identificar números coprimos.
- A Notação Sigma. Um símbolo para os somatórios definidos.
- A Notação Científica. Representando valores, de forma padronizada, com potências de base 10.







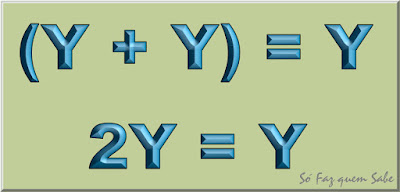

Se tivesse o botão de curtir, eu ia curtir! Excelente demonstração e reflexão, professor!
ResponderExcluirAo admitir que X=Y , voce não pode dividir a equação por (X-Y) pois seria o mesmo que dividir por 0
ResponderExcluirLegal relembrar a matemática dos bons anos 70, professores Elias, Teresa, Nicola, Bárbara... eeh saudades.
ResponderExcluirfechaed